Mean Variance Optimization
Modern Portfolio Theory,
Markowitz Portfolio Selection
Overview
The material presented here is a detailed discussion of Mean Variance Optimization (MVO) and Modern Portfolio Theory (MPT) in both single and multi-period contexts. It is also intended to help you decide which of the two MVO products, VisualMvo or MvoPlus, you might consider for your investments.
Contents
1. Introduction
4. Which Product is Right for You?
5. References
1. Introduction
The fundamental goal of portfolio theory is to optimally allocate your investments between different assets. Mean variance optimization (MVO) is a quantitative tool that will allow you to make this allocation by considering the trade-off between risk and return.
In conventional single period MVO you will make your portfolio allocation for a single upcoming period, and the goal will be to maximize your expected return subject to a selected level of risk. Single period MVO was developed in the pioneering work of Markowitz.
In multi-period MVO, we will be concerned with strategies in which the portfolio is rebalanced to a specified allocation at the end of each period. Such a strategy is sometimes called Constant Proportion (CP), or Constant Ratio Asset Allocation (CRAAL). The goal here is to maximize the true multi-period (geometric mean) return for a selected level of risk.
The material on multi-period MVO is largely based on the research manuscript Diversification, Rebalancing, and the Geometric Mean Frontier by William J. Bernstein and David Wilkinson [2].
2. Single Period MVO
Single period portfolio optimization using the mean and variance was first formulated by Markowitz. A key concept in this work was to identify the standard deviation (the square root of the variance) of a portfolio as a measure of its risk.
Markowitz Portfolio Optimization
The single period Markowitz algorithm solves the following problem:
Single Period Problem
The efficient frontier is conventionally plotted on a graph with the standard deviation (risk) on the horizontal axis, and the expected return on the vertical axis. A useful feature of the single period MVO problem is that it is soluble by the quadratic programming algorithm, which is much less CPU intensive than a general non-linear optimization code. This is the method implemented in VisualMvo.
The Markowitz algorithm is intended as a single period analysis tool in which the inputs provided by the user represent his/her probability beliefs about the upcoming period. In principle, the user should identify a number of distinct possible "outcomes" and assign a probability of occurrence for each outcome, and a return for each asset for each outcome. The expected return, standard deviation, and correlation matrix may then be computed using standard statistical formulae.
More informally, the expected return represents the simple (probability weighted) average of the possible returns for each asset, and the standard deviation represents the uncertainty about the outcome. The correlation matrix is a symmetric matrix, with unity on the diagonal, and all other elements between -1 and +1. A positive correlation between two assets A and B indicates that when the return of asset A turns out to be above (below) its expected value, then the return of asset B is likely also to be above (below) its expected value. A negative correlation suggests that when A's return is above its expected value, then B's will be below its expected value, and vice versa.
Two asset example
The basic principles of balancing risk and return may already be appreciated in a two-asset portfolio. Consider the following example:
| Asset |
Expected return |
Standard deviation |
Correlation matrix | |
|---|---|---|---|---|
| Asset 1 | Asset 2 | |||
| Asset 1 | 10.0% | 10.0% | 1.0 | -1.0 |
| Asset 2 | 13.0% | 30.0% | -1.0 | 1.0 |
In the two-asset case, the optimizer is not really necessary; all that is required is to plot the risk and return for each portfolio composition. The actual output presented here is adapted from that of VisualMvo (the dotted portion of the curve, and the labeling of the percentage of Asset 2 in portfolios A through E have been added).
Looking at the input data, it might appear that the small excess expected return (13% rather than 10%) of Asset 2 does not justify the considerable extra risk (a standard deviation of 30% rather than 10%), and that an investor should therefore select a portfolio consisting only of Asset 1. But the following MVO diagram paints a different picture.
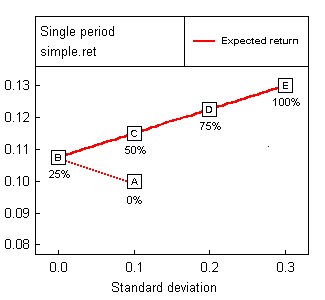
We see that as we start from Portfolio A (100% Asset 1) of the plot and begin to include some Asset 2, not only does the expected return increase, as we would expect, but the risk actually decreases until we reach Portfolio B at 25% of Asset 2. This "minimum variance" portfolio actually has zero risk (this is possible because the assets are assumed to be 100% negatively correlated).
The efficient frontier runs from Portfolio B, the minimum variance portfolio, to Portfolio E, the maximum return portfolio. An investor should select a portfolio on the efficient frontier in accordance with his/her risk tolerance.
Note that the maximum return portfolio consists 100% of the highest returning asset (in this case Asset 2). This is a general feature of single period mean variance optimization; while it is often possible to decrease the risk below that of the lowest risk asset, it is not possible to increase the expected return beyond that of the highest return asset.
Input Data Issues
A major issue for the methodology is the selection of input data, and one possibility for generating the MVO inputs is to use historical data. The simplest way to convert N years of historical data into MVO inputs is to make the hypothesis that the upcoming period will resemble one of the N previous periods, with a probability 1/N assigned to each.
The use of historical data provides a very convenient means of providing the inputs to the MVO algorithm, but there are a number of reasons why this may not be the optimal way to proceed. All these reasons have to do with the question of whether this method really provides a valid statistical picture of the upcoming period. The most serious problem concerns the expected returns, because these control the actual return that is assigned to each portfolio.
Failure of underlying hypothesis
When you use historical data to provide the MVO inputs, you are implicitly assuming that
These hypotheses may simply not be true. The most serious inaccuracies arise from a phenomenon called mean reversion, in which a period, or periods, of superior (inferior) performance of a particular asset tend to be followed by a period, or periods, of inferior (superior) performance. Suppose, for example, you have used 5 years of historical data as MVO inputs for the upcoming year. The outputs of the algorithm will favor those assets with high expected return, which are those which have performed well over the past 5 years. Yet if mean reversion is in effect, these assets may well turn out to be those that perform most poorly in the upcoming year.
If you believe strongly in the "efficient market hypothesis", you may not believe that this phenomenon of mean reversion exists. However, even in this case there is need for caution, as discussed in the next two sub-sections.
Error in the estimated mean
Even if you believe that the returns in the different periods are independent and identically distributed, you are of necessity using the available data to estimate the properties of this statistical distribution. In particular, you will take the expected return for a given asset to be the simple average R of the N historical values, and the standard deviation to be the root mean square deviation from this average value. Then elementary statistics tells us that the one standard deviation error in the value R as an estimate of the mean is the standard deviation divided by the square root of N. If N is not very large, then this error can distort the results of the MVO analysis considerably.
The true long term return
Suppose you believe that neither of the previous two problems is too serious. Then you will also believe that if you apply the MVO method in period after period, then the inputs that you use in each period will be more or less the same. Consequently, the outputs in each period will also be much the same, and so, by repeatedly applying your single period strategy, you will effectively be pursuing a multi-period strategy in which you rebalance your portfolio to a specified allocation at the beginning of each period.
It is then reasonable to hope that the expected return given by the Markowitz algorithm for your chosen portfolio will be the return that would actually have been obtained by this rebalancing strategy in the past, and thus also, by hypothesis, in the future. Unfortunately this is not the case; the expected return assigned by the algorithm to each portfolio is always an over-estimate of the true long term return of the rebalanced portfolio. Since this discrepancy increases as the standard deviation of the portfolio increases, the Markowitz efficient frontier always exaggerates the true long term benefit of bearing increasing risk. The moral here is to be wary of the rightmost part of the curve.
It is sometimes believed that this discrepancy is due to the fact that the single period MVO algorithm does not consider rebalancing. This is not correct; the origin of the problem lies entirely in the distinction between the arithmetic and geometric mean return. The problem can only be resolved by an extension of MVO into a multi-period framework (see Section 3).
Summary
The above discussion does not mean to imply that the Markowitz algorithm is incorrect, but simply to point out the dangers of using historical data as inputs to a single period optimization strategy. If you make your own estimates of the MVO inputs, based on your own beliefs about the upcoming period, single period MVO can be an entirely appropriate means of balancing the risk and return in your portfolio.
3. Multi-Period MVO
As we have seen, a major deficiency of the conventional MVO algorithm in a multi-period context is that, when used with historical data, the expected return that is assigned to each portfolio does not represent correctly the actual multi-period return of the rebalanced (or for that matter the unrebalanced) portfolio.
We begin our discussion of multi-period MVO by considering the analysis of historical data.
Two Asset Example
Consider the following two-asset, two-period example:
| Asset |
1996 return |
1997 return |
Arith mean |
Geo mean |
Std dev |
|---|---|---|---|---|---|
| Asset 1 | 0.0% | 20.0% | 10.0% | 9.54% | 10.0% |
| Asset 2 | 43.0% | -17.0% | 13.0% | 8.94% | 30.0% |
It is easy to check that under the hypothesis that the upcoming period will resemble 1996 or 1997, each with equal probability, this data leads to the MVO inputs considered in the single period two-asset example above. As in the single period case, the optimizer is not really required here; all that is necessary is to plot the risk and return for each rebalanced portfolio composition.
The output below is adapted from that of MvoPlus (the dotted portions of the curve, and the labeling of the percentage of Asset 2 in portfolios A through E have been added).

Comparing this plot with the single period one, we see some notable differences. The returns of all the portfolios are considerably smaller, and Asset 2 has a lower geometric mean than Asset 1, whereas it had a higher arithmetic mean. Nevertheless, as we increase the allocation of Asset 2 from 0% at Portfolio A, the geometric mean of the rebalanced portfolio increases, as did the arithmetic mean.
More significantly, we see that the rebalanced portfolio with the highest geometric mean return, which occurs close to Portfolio C, has a return of around 11.0%, which is considerably higher than that of either of the two individual assets.
This is very different from the single period case, in which any portfolio expected return must always lie below that of the asset with the highest expected return. This enhanced geometric mean is only possible because of the rebalancing; without rebalancing it is impossible to obtain a geometric mean return higher than that of the highest geometric mean return asset.
Lastly, we see that portfolios to the right of the maximum at 50% composition have increasing risk and decreasing return; this feature is not seen in the corresponding single period analysis.
Multi-Period Optimization with Historical Data
When generalized to multiple assets, the most natural problem to attempt to solve with historical data is
Multi-period Problem A
This is a mathematically well posed optimization problem, which may be solved exactly using the optimization capability of various spreadsheet programs. However:
Let us rather consider the following problem, which requires a less extensive set of inputs.
Multi-period Problem B
Unfortunately, Problem B is not easy to solve. In fact it is not even completely well posed, because the input data do not uniquely determine the geometric mean return of any given rebalanced portfolio.
A clue to finding an approximate solution to Problem B is to consider the analogous problem with arithmetic means:
Multi-period Problem C
This problem is exactly soluble by quadratic programming methods. In fact, it is already solved by the standard single period MVO algorithm!
This is because when we assume that the single upcoming period will resemble one of the previous N periods, each with equal probability, the expected return and standard deviation that are assigned to any given portfolio allocation are precisely equal to the arithmetic mean and standard deviation of the portfolio that was rebalanced to the specified mix at the beginning of each period.
This exact mathematical result provides the conceptual link between the single and multi-period versions of MVO.
Attempt to Solve Problem B
One popular attempt to solve Problem B is to retain the standard Markowitz algorithm, but to use as return inputs for the individual assets not the arithmetic means of the annual returns, but rather the geometric means. Unfortunately, this apparently plausible approach lacks any mathematical validity.
Firstly, just as the Markowitz algorithm with arithmetic mean inputs always overestimates the true return of any given rebalanced portfolio, the same algorithm using geometric mean inputs always underestimates the true return.
Secondly, the algorithm still produces a maximum return portfolio consisting of a single asset (in this case the one with the highest geometric mean), while we have seen in the above two-asset example that the rebalanced portfolio with the highest geometric mean return is sometimes a mixture of the assets.
Lastly, and most important, the weighted geometric mean does not represent any meaningful property of the rebalanced (or unrebalanced) portfolio with the given composition, while the weighted arithmetic mean does at least correctly represent the arithmetic mean return of the rebalanced portfolio.
A Better Solution
A much better way to solve Problem B is to exploit the existence of approximate relationships between the arithmetic and geometric mean. The mathematical foundation of the method is explained in Reference [2].
The essential idea is to use the relationship between the arithmetic mean and geometric mean to convert a Type B problem involving geometric means into a Type C problem involving arithmetic means. At the end of the calculation, the inverse relationship is used to convert the portfolio arithmetic means back to geometric means. This is the method used in MvoPlus.
An important feature of the methodology is the fact that, to a good approximation, the set of portfolios that optimize the rebalanced geometric mean are the SAME as the ones that optimize the arithmetic mean. This makes it possible for MvoPlus to display a combined plot of the Arithmetic Mean Frontier and the Geometric Mean Frontier.
The actual relationship between the arithmetic and geometric mean used in MvoPlus is different from those described in Reference [2], though the differences are small unless the assets are very volatile.
A solution to Problem B is only useful if it can be shown to provide a reasonable approximation to the solution of Problem A when full historical data is available; this is demonstrated empirically in Reference [2].
MvoPlus and the Future
The solution to problem B embodied in MvoPlus may be used as an optimization tool for the future. The process may be conceptualized in two different ways:
Deterministic Viewpoint
In this picture, the user makes forecasts of the geometric mean, standard deviation and correlation matrix for some specified range of periods in the future, and the output of MvoPlus, in particular the Geometric Mean Frontier, is that which would obtain if these forecasts turned out to be correct. In this viewpoint, the future is conceptualized in precisely the same way as the past.
Statistical Viewpoint
This picture is more similar to the conventional single period one. The user assumes that the different periods in the future are independent and identically distributed according to the specified inputs. Under this hypothesis, the interpretation of the geometric mean that is assigned to each rebalanced portfolio is that it is both the most probable return and the median return that would be obtained over a large number of periods.
Although these two viewpoints are conceptually rather different, the methodology for computing the Geometric Mean Frontier is the same in both cases, and the outputs of MvoPlus may be viewed in either way.
MvoPlus and Historical Data
When used with full historical data, MvoPlus operates in a slightly different way, called DATA mode, which combines the features of a mean variance optimizer and a back-tester of historical data.
First, the input data for Problem C are generated from the historical data, and the Arithmetic Mean Frontier is computed. The geometric mean of each portfolio on the frontier is then computed exactly using the historical data; this yields the Geometric Mean Frontier.
This approach again uses the fact that the portfolios that optimize the rebalanced geometric mean are, to a good approximation, the same as those that optimize the geometric mean, but provides a more accurate solution to Problem A than using the approximation between the geometric and arithmetic mean to compute the Geometric Mean Frontier.
4. Which Product is Right for You?
Single Period - VisualMvo
VisualMvo provides an implementation of the classical single period MVO algorithm. You should consider VisualMvo if either of the following applies:
Multi-Period - MvoPlus
MvoPlus has all the features of VisualMvo, plus the ability to optimize for multi-period geometric mean return of rebalanced portfolios. It also functions as a back-tester and approximate optimizer of historical data. You should consider MvoPlus if any of the following apply:
5. References
[1] Markowitz, Harry M., Portfolio Selection, second edition, Blackwell (1991).
[2] Bernstein, William J. and Wilkinson, David, Diversification, Rebalancing and the Geometric Mean Frontier, research manuscript (November 1997).