MvoPlus Sample Screen 1
DATA Mode

Valid HTML 5!
MvoPlus Sample Screen 1
MvoPlus Sample Screen 1

Description

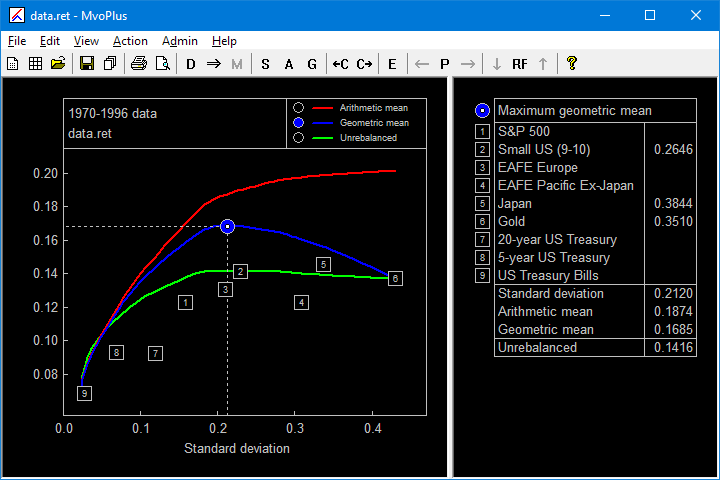
The main MvoPlus screen, showing the efficient frontier plot on the left, and the properties of the currently selected portfolio in the table on the right.

In this example MvoPlus is functioning as a back-tester and approximate optimizer of historical data. The three curves represent the properties of the "efficient portfolios".  These portfolios are constructed to maximize the arithmetic mean return when the portfolio is rebalanced at the end of each year. To a good approximation they also maximize the rebalanced geometric mean return. The geometric mean return of the rebalanced portfolio is shown in the blue curve. The green curve shows the return of the corresponding unrebalanced portfolio.

The selected portfolio is the one with the maximum value of the geometric mean; its properties are shown in the table on the right. In the plot, the currently selected feature (note the blue check mark in the legend) is the geometric mean, and this is the feature that is displayed for each asset (the numbered squares on the plot). The properties of each asset may be displayed in the table by clicking on the corresponding symbol on the plot or table.

The following points may be of interest:

  • The red "arithmetic mean" curve is identical to the conventional single period efficient frontier that would have been obtained on the hypothesis that the upcoming year would resemble one of the 27 previous years, each with equal probability. Click here to view the corresponding VisualMvo output.
  • The blue "geometric mean" curve always falls below the red "arithmetic mean" curve. In addition, the geometric mean has a maximum at a standard deviation of 21.2%; at higher standard deviations the geometric mean return actually decreases.
  • The maximum geometric mean return of 16.85% is greater than that of any of the individual assets.
  • Except at low return/standard deviation, the green "unrebalanced" curve falls below the blue "rebalanced" curve. When the individual assets have similar geometric mean returns (as the 6 stock assets do here), rebalancing is always beneficial, and there always exist rebalanced portfolios with greater geometric mean return than any of the individual assets.